https://www.acmicpc.net/problem/20444
20444번: 색종이와 가위
첫 줄에 정수 n, k가 주어진다. (1 ≤ n ≤ 231-1, 1 ≤ k ≤ 263-1)
www.acmicpc.net
- 색종이를 자를 때에는 한 변에 평행하도록
- n번의 가위질을 했을 때 k개의 색종이 조각을 만들 수 있을까?
- n번의 가위질 (1 ≤ n ≤ 2^31-1)
- k개의 색종이 조각 (1 ≤ k ≤ 2^63-1) : long형 변수
아이디어
0.1초라는 적은 시간에 넓은 탐색 범위 안에서 최적의 조건을 찾아야 하므로 이분탐색으로 먼저 접근해보았다.
n번의 가위질을 했을 때 k개의 색종이 조각을 만들 수 있는 지 판단해야 한다.
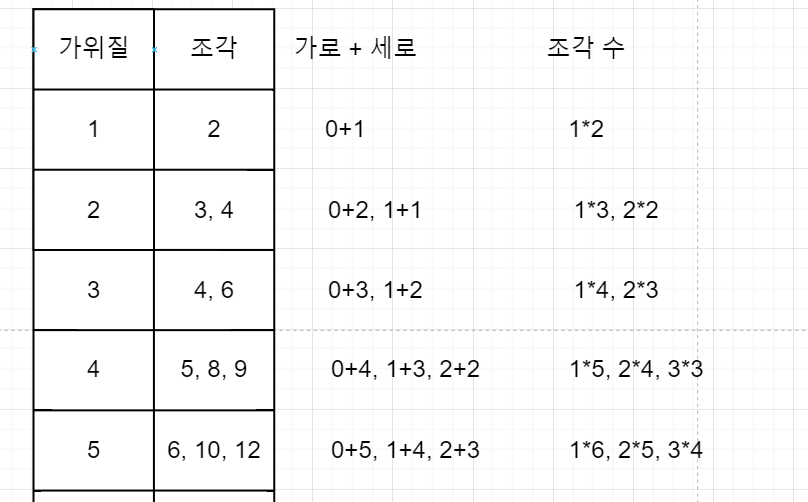
하나씩 해보니 아래와 같은 규칙을 발견했다.
- 가위질 수 = (가로로 자르는 횟수) + (세로로 자르는 횟수)
- (가로로 자르는 횟수, 세로로 자르는 횟수) 쌍의 경우의 수 = 조각의 경우의 수 (가로 <= 세로)
- (가로로 자르는 횟수+1) x (세로로 자르는 횟수+1) = 색종이의 조각 수
그렇다면 가로로 자르는 횟수를 매개변수로 설정한 후 이분탐색을 통해 K값을 찾으면 가능한 것이므로 찾으면 YES를, 못찾으면 NO를 반환해주면 될 것이다.
이분탐색의 범위는 가로로 자르는 횟수의 최소 값이 0이고, 최대 값이 N/2 이하이므로 0~N/2가 된다.

시간 복잡도
- 이분탐색의 범위가 0~N/2이므로 시간 복잡도는 O(log N/2)이 걸린다.
- N의 최댓값은 2^31이므로 O(log 2^30)이라서 시간 내에 풀이가 가능하다.
구현
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
static int N;
static long K;
static void init() throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
N = Integer.parseInt(st.nextToken());
K = Long.parseLong(st.nextToken());
}
static void pro() throws IOException {
int L = 0;
int R = N / 2;
while (L <= R) {
int mid = (L + R) / 2;
if (paper(mid) > K) {
R = mid - 1;
} else if(paper(mid) < K){
L = mid + 1;
// 찾은 경우
} else if(paper(mid) == K){
bw.write("YES"+" ");
return;
}
}
bw.write("NO"+" ");
}
static long paper(long mid) {
long row = mid;
long col = N - row;
return (row + 1) * (col + 1);
}
public static void main(String[] args) throws IOException {
init();
pro();
bw.close();
}
}
'Algorithm > 이분탐색' 카테고리의 다른 글
| BOJ 3079 - 입국심사 (0) | 2022.05.12 |
|---|---|
| BOJ 6236 - 용돈 관리 (0) | 2022.05.09 |
| BOJ 2343 - 기타 레슨 (0) | 2022.05.09 |
| BOJ 2110 - 공유기 설치 (0) | 2022.05.08 |
| BOJ 2512 - 예산 (0) | 2022.05.02 |
