류호석님의 패스트캠퍼스 강의 자료를 참고하여 정리한 글입니다.
출처 : https://github.com/rhs0266/FastCampus
완전 탐색
문제 해결을 위해 모든 경우를 전부 탐색하는 방법으로 정답을 무조건 구할 수 있다.
장점 : 부분 점수를 얻기 좋음
단점 : 모든 경우의 수를 전부 탐색하기에 시간 복잡도가 높음
완점 탐색 종류
- N개중 중복을 허용하여 M개를 순서 있게 나열하기 : 중복순열
- N개중 중복없이 M개를 순서 있게 나열하기 : 순열
- N개중 중복을 허용하여 M개를 고르기 : 중복조합
- N개중 중복없이 M개를 고르기 : 조합
완전 탐색 문제 접근 시
- 고를 수 있는 값의 종류 파악
- 중복 여부
- 순서를 따지는 지
N개중 중복없이 M개를 고르기 : 조합
백준 15652) N과 M (2) https://www.acmicpc.net/problem/15650
15650번: N과 M (2)
한 줄에 하나씩 문제의 조건을 만족하는 수열을 출력한다. 중복되는 수열을 여러 번 출력하면 안되며, 각 수열은 공백으로 구분해서 출력해야 한다. 수열은 사전 순으로 증가하는 순서로 출력해
www.acmicpc.net
1) 아이디어
백트래킹으로 모든 경우의 수를 탐색한다.
중복없이 고르기만 하는 조합이므로 a, b와 b, a는 같은 케이스이다.
중복없이 : visit[] 배열로 방문처리를 해서 중복을 방지한다.
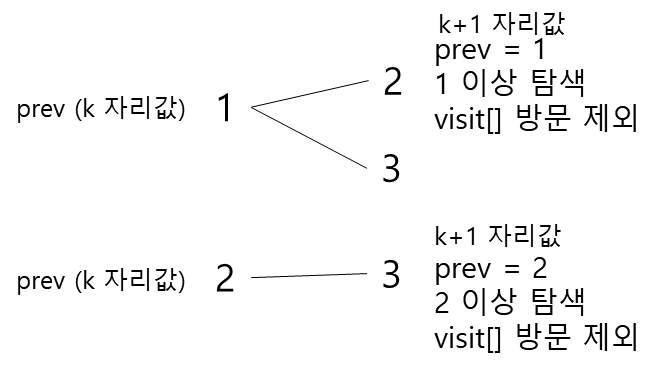
고르기 : 1부터 탐색한다고 했을 때 k+1의 자리값은 k 자리값보다 크도록 k 자리값인 prev 변수를 넘겨주어 다음 선택지에서 prev보다 큰 케이스만 고려할 수 있도록 한다.
2) 시간 복잡도 계산
N과 M의 조합 즉 nCm이므로 조합 공식 적용 O(nCm)

N과 M의 최대값이 8이니까 O(8!/(4!*4!)) < 1억
3) 구현
// 언어 : JAVA , (성공/실패) : 1/0 ,
// 메모리 : 15848 KB , 시간 : 140 ms
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
static int N, M;
static int[] selected, visit;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
// M개 고를건데 편의상 1부터 할거라서 M+1로 잡아둠
selected = new int[M + 1];
// 1~N개의 자연수 방문처리
visit = new int[N + 1];
// 중복조합 구하는 재귀 호출
rec_func(1, 1);
bw.close();
}
private static void rec_func(int k, int prev) throws IOException {
// 한 케이스에 대해서 M개 다 골랐으면
if (k == M + 1) {
for (int i = 1; i <= M; i++) {
bw.write(selected[i] + " ");
}
bw.write("\n");
} else {
for (int i = prev; i <= N; i++) {
if(visit[i] == 1) continue;
// 선택 후 방문처리
selected[k] = i;
visit[i] = 1;
// 완전탐색
rec_func(k + 1, i);
// 초기화
selected[k] = 0;
visit[i] = 0;
}
}
}
}
다른 사람들 코드 보니까 방문처리를 안하고 prev대신 prev+1부터 탐색해서 더 간단하게 구했더라..
// 언어 : JAVA , (성공/실패) : 1/0 ,
// 메모리 : 15848 KB , 시간 : 140 ms
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
static int N, M;
static int[] selected, visit;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
// M개 고를건데 편의상 1부터 할거라서 M+1로 잡아둠
selected = new int[M + 1];
// 중복조합 구하는 재귀 호출
rec_func(1, 1);
bw.close();
}
private static void rec_func(int k, int prev) throws IOException {
// 한 케이스에 대해서 M개 다 골랐으면
if (k == M + 1) {
for (int i = 1; i <= M; i++) {
bw.write(selected[i] + " ");
}
bw.write("\n");
} else {
for (int i = prev; i <= N; i++) {
// 선택
selected[k] = i;
// 완전탐색
rec_func(k + 1, i+1);
// 초기화
selected[k] = 0;
}
}
}
}'Algorithm > 완전탐색' 카테고리의 다른 글
| BOJ 14888 - 연산자 끼워넣기 (0) | 2022.02.22 |
|---|---|
| [완전탐색] BOJ 15654 N과 M (5) (0) | 2022.02.16 |
| [Algorithm] 완전탐색 - 중복조합 (0) | 2022.02.16 |
| [Algorithm] 완전 탐색 - 순열 (0) | 2022.02.14 |
| [Algorithm] 완전 탐색 - 중복순열 (0) | 2022.02.14 |
![[Algorithm] 완전탐색 - 조합](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FxlB56%2FbtrtsUKHLCg%2Fy9ommr6gmTKjBlNulBwjRK%2Fimg.png)